Selecting and Sequencing Equitable Discourse with Desmos

Note, this post is from a presentation I gave at ISTE 2019, NCTM Boston 2019, NCTM Nashville 2019, and ATOMIC 2019. Thank you to all that attended!

The Five Practices

In 2011, Mary Kay Stein and Margaret Smith wrote and published the Five Practices for Orchestrating Productive Mathematical Discussions. This book describes one instructional routine for getting students to more meaningfully discuss their ideas in math class. Over the past few years, it has influenced many math teachers and math teacher leaders, and has become a seminal book. In fact, a “5 practices for science” came out a couple of years ago. If you have anything to do with STEM education, I would absolutely recommend you read this book.

In any case, Smith and Stein describe five teaching practices that promote student learning:

• Anticipate ideas students will produce during a task or activity
• Monitor student work during class for those ideas and others that weren’t anticipated
• Select a subset of those interesting student ideas
• Sequence the order of their presentation, and then help students
• Connect them through discussion

Now, you don’t need Desmos to do a 5-practice routine. In fact, I use the five practices often without Desmos. Here’s what that looks like:

I start with a task. For example, I might want my students to try the "height of waist off ground" task task from Graphing Stories by Dan Meyer and Buzz Math.

Then I create a graphic organizer, such as this one:

Before the lesson starts, I anticipate the various solutions students will come up with.

During the lesson, I showed my class the video and asked them to draw the graph with pencil and paper. As they did, I would walk around and take note of their solutions.

In orange, I recorded that Phil, Kim, and Dan all had the “Stand” portion of the graph, but that it looked different. I noted that so I could come back to it for a discussion.

As students were finishing, I thought about how which work samples I had time for, and what sequence I would put them in. My objective here was to move from less precise graphs to more precise graphs, so I chose a sequence that would build towards this objective.

Finally, I would bring student work to the front of the room and ask students connecting questions. This might be a bit hard to see, unless I had a document camera or had students work on chart paper.

So, if the five practices are good on their own, what value does Desmos add?

Anticipate

What value does Desmos add to the anticipating step? You might think not much. After all, you still need to do the task yourself beforehand to anticipate how students will solve it. Desmos can't do the task for you!

However, in the bottom left corner of each teacher screen, Desmos activities have “Teacher Moves” that often include Pedagogical Moves, Sample Responses, and Student Supports. They’re definitely not meant as an answer-key, but they’re good to read when you’re doing your own activity for the first time.

Monitor

When I do a 5-practice routine on paper, sometimes I struggle to get to every student or every group. When I am able to get to a group, I’m often going in blind. I have to stand over the student’s shoulder, read through their work, and then think of a thoughtful question or prompt before I actually engage with the student.

Desmos classroom activities bring monitoring to a whole new level. I can quickly scan through the summary dashboard to see what task students are currently working on.

I can use the teacher dashboard to see all my student’s responses to a particular question, identify which students need verbal prompting, and what the prompt should be before I walk over to the student. Remember, the goal of classroom activities is not to put kids on a platform and let them go. The goal is to promote discussion, even during monitoring.

This also brings up the idea of equity. I know that I have some degree of bias when I’m walking around the room looking at student work. There are definitely some students that I’m going to check-in on more often than others, because I know they struggle. But, this might cause me to miss a different student who needs some help, or a student with a great idea that is worth sharing with the class. With the teacher dashboard, I can see everyone’s work. This allows me to make more equitable decisions about who I talk to and what I say.

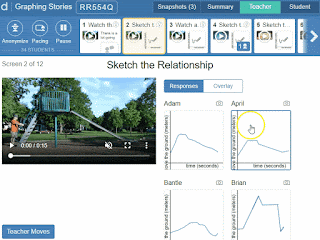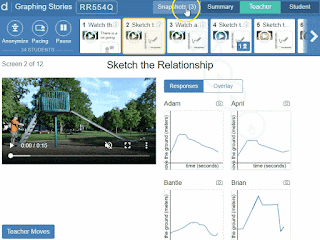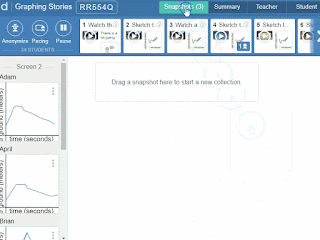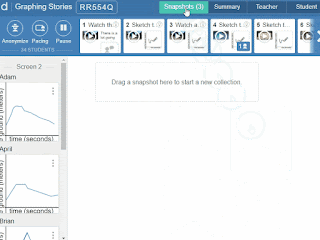
I can click any of these to see the student’s work a bit larger.

The overlay button is can also be helpful to see all of my student’s work at once to look for trends.

There are also three more features that help with monitoring. If I need to gather student attention to make a clarifying comment, I can use the pause button. This will freeze student’s current screen, and often garners moans and boo’s from the class.

I can also limit which screens you can visit by using the teacher pacing button. By default, Desmos activities are student-paced. But you can lead students through part of an activity one screen or section at a time. You click the button and choose which screens to restrict students to.

If you want to share student work from the teacher dashboard, but you don’t want students to know whose work it is, use the anonymize button. It will change every student’s name to the name of a famous mathematician or scientist.

This also helps to make the discussion more equitable. When I class of students to volunteer their answers, a few hands shoot up immediately. I give some wait time to allow more students the opportunity to volunteer. But, even with all the wait time in the world, some students don’t want to volunteer their answers because they don’t feel they have the status in the math classroom to do it. By taking away student names, we also take away some of the issues with status and show students that all ideas are valuable and worth examining.

More information on all these tools can be found here.

Select, Sequence, Connect

If you see interesting ideas you might want to select at any time during an activity, press the camera icon next to it.

Then go to the “Snapshots” tab.

Sequence the ideas by dragging them into a collection.

Add a comment or a question to help students connect their classmates’ ideas to the main ideas of the lesson.

And display them.

More information on snapshots can be found here.

So, why is all this important?

Why Open Ended Insight?

Mathematical thinking is complicated, especially deep mathematical thinking that comes from open-ended tasks. Other online math platforms attempt to triangulate student’s understanding through a series of multiple choice questions. And while this may have its place, mathematical thinking is far too messy to be evaluated using a series of multiple choice options. We need to wrestle with the misconceptions that students have and grow their thinking. Desmos allows us to see what students are actively working on, and then invites us to have a real-life conversation about it.

Why Student Work?

Students pay much more attention to discussions when the discussion isn’t about a page from the textbook or a worked example from the teacher but about ideas from the students themselves. It’s the difference between “Here's how to find the area of a Triangle” and “Here are a few methods to find the area of a triangle that you investigated. Which ones are best, and under what conditions?”

Why the 5 Practices?

We have limited time and limited resources, and a show-and-tell or gallery walk often takes a large amount of time. The point here is to make our discussions more equitable, and that doesn’t mean giving all students equal time to present.

Second, by selecting and sequencing student work, we convey our objective to students and what is important for them to focus on during this lesson. The discourse that follows tells our students that the discussion and connections are just as important as the work they can do individually.

Lastly, we want students to understand that all ideas are valuable, and not just those who answer first or get the most points. Again, this is a tool to make our conversations more equitable and give all students status in the math classroom.

And speaking of discourse, there has been a boatload of research on the importance of using student to student discussions in developing and solidifying conceptual understanding.

What's Next?

• Check out a tutorial at learn.desmos.com. 

• See more of what desmos has to offer with this Desmos Smörgåsbord activity  I created. Go to student.desmos.com and use the class code: AXS2C5.

• Say hi on Twitter! I'm @MrJanesMath.

Encourage and Facilitate Growth with Standards Based Grading

I think it is important to encourage growth mindsets in students. That's why I allow students to retake content standards with no minimums or maximums (e.g. if a student achieves a 9/10, they can still retake). When a student does retake a content standard, they get different questions that assess the same "I can..." statement. I have also had students retake using different modalities as needed (e.g. whiteboards, desmos).

On the other hand, I rarely allow students to retake practice and scholarship standards. I tend to assess practice standards while students are working on collaborative tasks, and it is difficult to recreate the same situation after the fact.

By their very nature, scholarship standards must be assessed during a regular class. It wouldn't make sense for a student to be able to retake a scholarship standard. If they could, it would look a lot like "extra credit for extra work" - something that I have tried to steer clear of.

Finding time for Retakes

It can be hard to find ways to give students multiple opportunities to demonstrate their understanding in strictly traditional settings. The first school I attempted SBG in had a 30 minute advisory period in the middle of day. The schedule was set up so that most of my students had advisory at the same time as me (advisories were set up by grade). I would simply write students a pass, and they could see me for help studying, or to retake an assessment. There were some students that did not have advisory at the same time as me, and those students came into my room for their lunch or during their study halls.

The school I am also has an advisory period, but everyone has advisory at a different time. So, I’ve had to work to find time.

I’ve also set some rules. Only one standard can be re-tested per day, and You cannot receive tutoring right before you re-test a standard. I used to tell students they could only re-test twice, but it happens so rarely, it’s not worth discussing with students.

Grading Retakes

While some online grade books allow multiple grades for one assignment, with some sort of weighted average, my grade book does not. Once a student retakes a standard, I simply replace the old grade with the new grade and record the old scores in the comment section. Each student's grade reflects the most recent evidence of learning, and I put the old grades in the comment section.

Encouraging Growth with Visible Celebrations 

Students who score at least an 8/10 on a content standard are invited to sign a sheet of chart paper with the "I can..." statement written on it. It's a quick and public way to honor mastery without calling out those who do not sign the paper. Students who achieve an 8/10 on a retake can also sign the chart paper, and so there is an incentive to retake that some students are drawn to.

Encouraging Growth by Grading Formatives... Kinda...

Another interesting question is the role of formative assessment. Most experts believe that formative assessment is only for and feedback to the student, and should not be graded. I agree, but parents and administrators in more traditional settings like to see more grades. So, I put formative assessments in the grade book up until we take a summative assessment (i.e. content standard).

Once I put the summative assessment in, I uncheck the "count in final grade" box. The assignment stays in the book, but doesn't count towards the final grade. This way, students can see their progress without being penalized for it. And, there are plenty of assignments in the grade book... now everyone is happy.

Multiple Opportunities to Practice Independently

It's important that students have multiple opportunities to practice independently, whether you're in a traditional or standards based classroom. The nice thing about a standards based class is the opportunity to tag independent practice with the standards so that they are organized and easily accessible.

I put some nails in my wall (oops!) to create a "Practice Wall" of worksheets. When students need extra practice, they just pull out one of these. They mostly consist of practice I've already assigned for homework, but there is often a little bit extra. I post answer keys online and use the Homework Sandwich method from Bruce Jackson. While I do give feedback to students one-on-one, this lets them practice and get their own feedback whenever they're ready.

All the videos, formative assessments, and online answer keys all tagged with the same standard too. This makes it easier to go between them - the same number indicates the same standard. I also open up all of my online quizzes for unlimited re-trys (after I see the data from the first try in class) so that students can continue to practice and improve. Again, they're getting their own feedback.

But all of these opportunities have been about content. About once a week, we have can activity where students get feedback on practice standards. They are typically in the style of a five practice routines, and feedback could be verbal or written (using a practice standard rubric). Again, it's all about empowering the student to practice and giving formative feedback when they do.

Encourage Academic Habits and Reflection with Scholarship Standards

Many teachers who use standards based grading only count content (and maybe math practices) into the final grade. I think it’s important to think about effort and behavior, but in a way that makes sense with standards-based grading. I also wanted to personalize it to meet my student’s needs. I created a rubric that has 10 goals. Each quarter, students choose three goals, and reflect on each of their goals every class in a google form. At the end of each quarter, we meet and they can change their goals.

This gets translated into their scholarship grade. So, students are essentially grading themselves. There are students who need to be reminded they were late to class, or disorganized, but if you're paying attention, most students are honest.

Below is the worksheet that I give students. Here is an electronic version you could print. We typically start there, and then move to a google form once students are comfortable. You can actually have google send these reflections home to parents. Check out Marissa Walczak's post about it here.

However, don't feel that electronic is the only way to go. Normal paper works great, and if students keep a math journal, this can easily be integrated in.

---

Scholarship Goal Setting Document

The best way to improve in any field is to reflect in order to analyze your practice, find room for growth, and determine the most efficient way to improve. Math class is no different! Please read the goals below and identify three that you think that will help you grow the most. If you feel there are more than three you want to focus on, choose goals closer to the top of the list.

Each class, you will reflect on your three goals with a google form. You will be asked to rate yourself using the language found in the rubric below. At the end of the reflection, you will think about what you can do to improve on your goals. These reflections will be used as part of your scholarship grade, and I will conference with you periodically about your reflection and growth. If you feel that you are having difficulty with your goals, or believe you have mastered one or more of your goals, please meet with me to discuss changing your goals before the next unit.

Goal	Not There… Yet! (0 points)	Getting There (½ point)	Met Goal (1 point)
Punctual	I was more than a minute late to class, including getting my materials	I was less than a minute late to class, including getting my materials	I was on time to class and started the warm up immediately.
Prepared	The teacher needed to remind me to go get my materials	I asked the teacher to get my materials or provide extra materials	I had all of my materials at the start of class, including video notes and homework
Focused	I was not focused, even after redirection from the teacher	I needed some redirection from the teacher	I was focused without redirection from the teacher
Transitions	I needed to be reminded how to transition from one activity to the next	I transitioned from one activity to the next with some talking or distraction	I transitioned from one activity to the next without any talking or distraction
Organized	I was unable to find all of my materials	It took me a few seconds to find some of my materials, and I needed to be reminded to use them	I was able to find all my materials easily and use my tools (notes, calculator, whiteboard) strategically
Self-Starter	I needed to be reminded to start a problem	I started a problem, but needed reminding when it became too difficult	I started problems quickly and persevered through difficult problems
Participate	I did not participate in class	I participated in class by talking to the teacher directly	I participated in class by responding to my classmates using talk moves
Precision	I did not use precise language today	I attempted to use precise mathematical language, but was sometimes inaccurate	I explained my ideas using precise mathematical language, both when writing and when speaking
Peer Tutor	I did not help others today	I helped others by reminding them of the steps needed to solve a problem	I helped others by explaining an idea conceptually and letting them solve the problem
Role Model	I was not a role model today	I served as a role model by demonstrating BARK	I served as a role model by encouraging others to act with belief, awareness, respect, and kindness

Push Students to Work like Mathematicians with Practice Standards

Practice standards come from assessments that measure progress towards one or more of the Common Core Standards for Mathematical Practice or other 21st Century Learning Skills. I typically assess these with with collaborative tasks or projects and grade them with a rubric. The tasks I use vary widely between formal performance tasks, group presentations, debates, modeling tasks, games of taboo and pictionary, error analysis, and more.

My rubrics also vary. The practice standard rubrics are out of 10 points, like my content standard rubrics, but the rows depend on the specific task students are doing and the skill I am trying to assess.

One thing that has become consistent is when I assess practice standards. I like to start units or topics with a collaborative anchor task that the rest of the unit can relate back to. I don't grade this anchor task, but I do give students feedback. Then, we go ahead with the regular lessons. Towards the end of the unit, I have students work on a task that is similar to the anchor task, and this time I grade it with practice standards.This has a few benefits:

• Student's level of anxiety is lower because they have already seen a similar anchor task
• The teacher can get a clear assessment of where they are at with the practice standards because content standards shouldn't be holding them back
• A collaborative task can serve as a good review for a summative assessment 
• Using similar tasks as bookends on a unit gives students a chance to reflect back and see how the mathematics they learned allowed them to dig deeper into a specific problem.

Focus on Assessing Concepts with Content Standards

I hate nickeling and diming students for points. I hate having students come back to me after an assessment and argue why I took off two points instead of one. I hate putting one grade on the front of a test, even though there were many skills that students needed to know to be successful. So, here's what I now do:

Before I start a unit, I identify the skills and knowledge students will need to be successful. I write them as student friendly "I can..." statements. These become my content standards, and I save these in a spreadsheet for later years. I also number them. A few are below.

Standard 10: I can specify a series of transformations that carry one figure onto another.

Standard 15: I can apply the Pythagorean Theorem to solve a variety of geometric problems.

Standard 21: I can find and interpret the slope of a line in a variety of representations

Then, I take my old tests and quizzes and place the assessment items (i.e. questions) into groups based on which of the standards they're assessing. Ideally, I have just enough items to allow me to accurately determine if a student has mastered that standard. Sometimes I have too many or not enough items, and I fix that by deleting some or writing more. For some reason, this often comes out to exactly one page. Below is an example.

Notice that there are no point values on each question. Instead of grading each question, I give written feedback. Then at the top, I give a holistic score at the top out of 10 points. Below is the rubric:

10/10 Above Mastery: you have mastered the skill and correctly applied it to a challenging and novel situation

9/10 Mastery: you have demonstrated a full understanding of the concepts involved, have clearly showed all steps of your reasoning, have used notation correctly, and have no errors

8/10 Some Procedural Errors: you have demonstrated a full understanding of the concepts involved, but you may have made a procedural error that was not related to this standard 

7/10 Some Conceptual Errors: you have demonstrated partial understanding, but are unclear on one minor concept.

5/10 Weak Understanding: you have attempted to answer the question, but are unclear about multiple minor concepts, or one key concept. Student should retake.

0/10 No Understanding: You left the page blank or made no mathematical attempt. Student should retake.

I once had another teacher jokingly rephrase it this way:

10/10 Above Mastery: Wow!

9/10 Mastery: Yes!

8/10 Some Procedural Errors: Yes, but…

7/10 Some Conceptual Errors: Kinda…

5/10 Weak Understanding: Not really.

0/10 No Understanding: Check for a pulse!

Why 10 points? 

Well, I've tried grading with the more common 4 or 5 column rubrics, but there is often confusion that a 3/5 means the same as a 60% in a 100-point grading system. That's a battle I kept having to fight with students and parents. However, by grading out of 10, students can easily match their grade up with the A, B, C, D, F format of most schools. I don't necessarily like the system, but I would rather my students not be confused.

What's the 10/10 all about?

Most standards based grading systems advocate for no extra credit. But, in classes with many different ability levels, teachers often feel the need to give students who go above and beyond some sort of credit. So, the “extra credit” is hidden in the 10/10. Students that demonstrate mastery still receive 9/10, but the challenge is there for students that want it. And, if students are unable to get the challenge question, they will still get a 9/10 - not a far way to fall.

What if a student gets the challenge question, but has mistakes elsewhere?

If a student had a minor computational error, but they got he challenge, I write "8+1/10" on their paper. the 8 is for the minor computational error, and the +1 is for the challenge question. They will end up with a 9/10 in the grade book, but I also put a note on the assignment. It's not a perfect solution, but gets the point across.

Where's the 6/10?

In my school, a 60% means that a student is just barely passing the course. Unfortunately, that makes it a very ambiguous grade for students. Does it mean that they skills and knowledge they need to succeed? Or, does it mean that they don't have the skills and knowledge, but they did just barely enough work to pass? To avoid confusion, I don't give 6/10. (see my first norming activity for more information)

Where's the 4/10, the 3/10, the 2/10, or the 1/10?

I allow students to retake assessments. If there is no understanding evident, then I need to strongly encourage the student to study and retake the assessment. I feel giving a 3/10 sends mixed messages to students and takes longer to grade.

How much time does it take to grade assessments this way?

I have found grading this way is faster than grading by question. That's because I don't perseverate over how many points I am allotting per question. I've also found I give better written feedback because I'm looking at the standard as a whole.

How many standards are on one test?

The sweet-spot for me seems to be three or four. I once did six, and it took too long. Just assessing one seems like a job for an exit-slip. We do give final and midterm exams, and for those I typically have six to eight standards.

So, how do you put grades into the grade book?

I put in one grade per standard, so students can see their level of mastery on different standards. I never average together all the standards, and I don't encourage students to do it either.

What does this mean for formative assessments?

I have started labeling formative assessments, independent practice, and collaborative tasks with wither the "I can..." standards or the number of the standard. That way, students can see how learning activities, formative assessments, and summative assessments all relate to each other. It also helps students find resources when studying or retaking assessments.

Do you retest the same standard throughout the year?

I reserve the right to retest any standard at any point during the year. In reality, I only retest key standards, ones that constitute the major work of the grade. Our school gives midterm and final exams, and the standards on those have all been tested before.

Three Types of Standards

I've done a lot of thinking about all the ways that students get feedback, including formal assessments, informal comments, and personal reflections. When you sit down to list them, there are quite a lot: written feedback on exit slips, verbal feedback from peers during group work, passing comments from me as I circulate around the room, a number in red at the top of a test, and so many more. Yet, I think I've settled on three general buckets for these types of feedback, or at least for the feedback I want to record as a grade. Below are the three buckets with some explanation to them. Click each one to find out more.

Content Standards

Content standards come from assessments that measure progress towards one or more of the Common Core Math Content Standards or any math-specific standards. This could also be called the “traditional” math grade. Typically, content skills and knowledge are not very transferable to other courses, except ones that directly use math content (e.g. physics).

Examples of assessments include exit slips, quizzes, tests, and content-specific tasks. There may be (and often is) more than one content standard per assessment. I typically assess three separate standards in one sitting.

Practice Standards

Practice standards come from assessments that measure progress towards one or more of the Common Core Standards for Mathematical Practice or other 21st Century Learning Skills. These could be seen by some as an “application” grade, but should could (and should) include all standards for mathematical practice such as justification and precision. Typically, these skills are transferable to other courses and other fields.

Examples of assessments include error analysis, collaborative group activities, modeling projects, and any task intended to measure the mathematical practices. Just like content standards, you could assess multiple practice standards in one assessment. In fact, many of my collaborative tasks include both content standards and practice standards.

Scholarship Standards 

Scholarship standards represents a student’s progress towards the transferable qualities of being a productive student. This includes "soft skills" such as executive functioning skills, punctuality and preparedness, working flexibly, self-monitoring, and reflection. Typically, these skills are transferable to all other academic settings. One example of a scholarship standard assessment is a personal reflection using a rubric.

How these Interact with a Traditional Grading Scheme

Unfortunately it can be hard to pull these three types of standards apart in the grade book, especially if you're working in a traditional system with an online grade book that averages all the grades together to get one final grade. If that's your reality, I suggest setting up your online grade book with these three buckets as categories. Then, when progress report or report cards get sent out, simply print out a category report. Then, you can:

• Send it home to parents so they can understand their student's specific strengths and areas for improvement
• Conference with the students one-on-one so they understand the connection between the categories (e.g. scholarship standards have an impact on content standards)
• Use it to help write comments on report cards (e.g. students with high practice standard scores often get something like "Works like a mathematician by collaborating with others, attending to precision, and persisting through challenges"

Now, I'm pretty sure this is all stolen. I vaguely remember reading about categorizing standards years ago, but I can't remember the source. So, if anyone can point me in the right direction, I would be happy to give credit where credit is due.